Difference equations converging to Pi
Highlights:
Historic:
"Proposion 3:
The circumference of any circle is three times the diameter
and exceeds it by less than one-seventh of the diameter and by
more than ten-seventyoneths"
- from Measurement of a Circle by
Archimedes
(287-212 BC).
Archimedes' approximation 22/7 to π is accurate
to an astonishing one part in 2484.
Mathematical: Hexagons are circumscribed and inscribed around a unit circle. The polygons are iteratively subdivided to give 12, 24, 48 and finally a pair of 96-gons. The semi-perimeters of these polygons give the upper and lower bounds for π, respectively. The semi-perimeters are iteratively approximated using trigonometric identities which Archimedes derives. These iterations are realized below as solutions of a set of difference equations.
Prerequisites:
None.Equations:
| x1 | → | x1+√(1+x12) |
| x2 | → | x2+√(1+x22) |
| x3 | → | 2 x3 |
| x4 | → | x3/x1 |
| x5 | → | x3/√(1+x22) |
Variables:
x1 : lower approximation of cotangent of π/n.
x2 : upper approximation of cotangent of π/n.
x3 : n, the number of sides of the polygons.
x4 : semi-perimeter of an n-gon circumscribed about a unit circle.
x5 : semi-perimeter of an n-gon inscribed in a unit circle.
Discussion:
Here we first outline the algorithm of Archimedes for approximating
π in a historical context.
Then we implement his algorithm in Phaser as a system of difference equations
and perform his computations on a modern computer.
In Measurement of a Circle Archimedes derived that π was between 3 1/7 and 3 10/71. None of Archimedes original works exist; however, references to his works by near contemporaries give confidence that the collections written centuries later, essentially as university textbooks, are accurate records of his thoughts.
His method was geometric. To establish a lower bound, he inscribes a regular hexagon inside a unit circle. By subdividing each face he arrives at a regular 12-gon, then 24-gon, and so on. As the number of faces increases, so does the perimeter of the polygons, and it approaches the value of 2π the circumference of the circle. The upper bound is established similarly using circumscribed polygons.
The process of subdivision halves at each step the angle φ formed by a polygon vertex, the center of the circle and the midpoint of a polygon face incident on the vertex. Archimedes did not use the notation of trigonometric functions. Greek mathematics used the ratios which only much later were given the names familiar today. For the process of subdivision, Archimedes derives the following two formulas,
Archimedes shows explicitly only the first of these identities. The second is inferred from his calculations. The two trigonometric identities can be combined into a single formula,
Let Pn be the semi-perimeter of a regular n-gon circumscribed around a unit circle. Let pn be the semi-perimeter of a regular n-gon inscribed in a unit circle. Then,
For a regular n-gon, φ=π/n.Archimedes starts with the rational approximations for the hexagon and uses the half-angle formula to get cot φ for φ=π/12, π/24, and so on. From the cotangent the semi-perimeters are calculated. With each square root, he was required to round to a rational. He carefully rounds in the direction which keeps the inequality correct.
The first calculation concerns the sequence of circumscribed polygons. To overestimate their area, it is necessary to underestimate cot φ, beginning with the underestimate of this value for the hexagon,
The second calculation concerns the sequence of inscribed polygons. Although the formula for pn shows only the dependence on the cosecant, the calculation proceeds based on the cotangent. Therefore, an overestimate is required,
Both calculations can begin with the exact value for the cosecant, so the first iteration gives the bounds,To continue to the next iteration, csc π/12 will be needed, and approximate square roots will be taken preserving the sense of the inequalities.
The computer also computes only with rational approximations to reals. We often take our best approximation and then ignore this discrepancy, computing as if the result is accurate. However, Archimedes was more thoughtful as he kept firm bounds, working each inequality separately.
Dynamics:
Phaser Simulation: In light of the historical account above, let us now revisit the five equations which we will iterate in Phaser simulations to approximate π .
The variables x1 and x2 are upper and lower approximations of the cotangent of π/n, starting with n=6 and doubling n with each iteration. The formulas for the cotangent half-angle is combined with the cosecant identity into the single formula,
The formulas are the same, but they begin at different initial conditions. The variable x3 follows n, beginning at 6 and doubling each iteration,
The variables x4 and x5 give Pn and pn, respectively. As such they should converge toward π. The semi-perimeter of the circumscribed polygon x4, by nature an overestimate to π, uses x1, the underestimate of the cotangent. Likewise, the overestimate x2 of the cotangent is used for x5, the semi-perimeter of the inscribed polygon. Their initial values are not important.
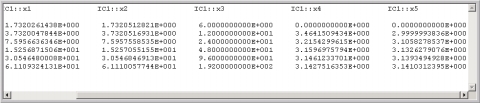
Figure 1. Upper (x4) and lower (x5) estimates to π .
To animate this image in your local Phaser, click on it.
Error Analysis: Assuming that the rounding errors are not too large, the cosecant formula can be used to give a simple analysis of the converge around π of the pair of semi-perimeters. Substituting equations (4) and (5) into equation (2),
Then, When n ≥ 6 we have the bounds, This gives error bounds decreasing as 1/n2, As a numerical illustration, for n = 96 the error bound is 0.00214184, and the actual error is,Suggested Explorations:
- Derive the cotangent half-angle formula (1). This can be derived from half-angle formulas for sine and cosine. Archimedes proved it directly from the geometry; see ROSENBERG, Lemma 2, for a reproduction of the proof.Compare the last values of x4 and x5 in Figure 1b to the fractional values 22/7 and 223/71 of Archimedes. What could be the cause of the discrepency?Load the Phaser project in Figure 1b into your computer and continue the iterations several more steps (set time=20). Do the upper and lower bounds converge to π = 3.14159265358979323846?The semi-perimeters of the polygons should converge to π = 3.14159265358979323846, but they do not. This is because approximate values for √3 are used as initial conditions. Use Phaser's Newton-Raphson MAP to compute a more accurate approximation to √3. Use this value as the initial condition for x1 and note the improvement in the resulting value for π.Archimedes began with hexagons. Change the initial conditions to begin with squares.
- Add an equation for the error. Verify the convergence rate.
Related Modules:
Gauss AGM Pi MAP -- Gauss and the fastest iteration to Pi.References:
ALFELD, P, Archimedes and the Computation of Pi,
http://www.math.utah.edu/~alfeld/Archimedes/Archimedes.htmlARNDT, J. and HAENEL, C. [2001]. π Unleashed, Springer-Verlag.
BERGGREN, L., BORWEIN, J., and BORWEIN, P. [1997]. Pi: A Source Book, Springer-Verlag.
DIJKSTERHUIS, E. J. [1987]. Archimedes, Princeton University Press.
GOURDON,X. and SEBAH, P, Numbers, Constants and Computation,
http://numbers.computation.free.fr/Constants/constants.htmlHEATH, T.L. [1897]. "Measurement of a Circle", in The Works of Archimedes,
Cambridge University Press, pp. 91-98, http://www.math.ubc.ca/~cass/archimedes/circle.htmlNOVA, Infinite Secrets,
http://www.pbs.org/wgbh/nova/archimedes/pi.htmlO'CONNOR, J. and ROBERTSON, E. F., Archimedes of Syracuse,
http://www-gap.dcs.st-and.ac.uk/~history/Mathematicians/Archimedes.htmlPHILLIPS, G. M., [1981], Archimedes the Numerical Analyst, in BBB [1997]. pp. 15-19.
ROSENBERG, B. [2003]. Archimedes and Pi,
http://www.phaser.com/modules/historic/archimedes/meas_circle.pdfTHE WALTERS ART GALLERY (Curator of Manuscripts), Archimedes Palimpsest,
http://archimedespalimpsest.org/Feedback:
Please write to us with your comments on this module.