A pioneering model of host-parasitoid interactions

Highlights:

Ecological: When it is assumed that host density is limited only by the parasitoid, and that the parasitoid is confined only to one host species, host-parasitoid relations result in large amplitude oscillations. Historically, this is the first significant host-parasitoid interaction model.

Mathematical: For most ecologically relevant parameter values and initial conditions, solutions spiral away from an unstable fixed point (source).

 

Prerequisites:

Host-Parasitoid Models, Fixed Points of 2D MAPs, and Linearization at Fixed Points of 2D MAPs.

Equations:

H_n+1 = k H_n e^{( -a P_n )}
P_n+1 = c H_n [1 - e^{( -a P_n )} ]

Variables
H_n : Density of host at generation n
H_n+1 : Density of host at generation n+1
P_n : Density of parasitoid at generation n
P_n+1 : Density of parasitoid at generation n+1

Parameters
k : Reproductive rate of host
a : Searching efficiency constant of parasitoid
c : Average number of viable eggs deposited by parasitoid on a single host

Discussion:

Nicholson-Bailey model is a special case of the general Host-Parasitoid Models with a specific form for the function f( H_n, P_n ) accounting for the fraction of hosts not parasited.

To determine a specific formula for f( H_n, P_n ), it is assumed that parasitoid searches randomly and can lay unlimited eggs. The description of the distribution obtained by placing objects (parasitoid eggs) into boxes (hosts) is the Poisson Distribution. The probability of not being parasited is the zeroth term in the Poisson Distribution, and is given by the formula

f( H_n, P_n ) = e ^{( -a P_t )}

where a is a parameter measuring the search efficiency of the parasitoid.

Dynamics:

The dynamics of this model is rather simple. Typical host and parasitoid populations exhibit oscillations when observed over many generations. When host versus parasitoid are plotted on the phase plane, a typical orbit spirals away from an unstable fixed point (source).

Phaser simulations:

• Figure 1a: A typical host history. H_n versus n (generation) is plotted.
• Figure 1b: A typical parasitoid history. P_n versus n is plotted, Note that parasitoid eventually goes to zero.
• Figure 1c: Host versus Parasitoid. H_n is plotted versus P_n. Notice that the orbit is spiraling away from an unstable fixed point.
• Figure 1d. Flow on the phase plane. One thousand orbits from randomly chosen initial conditions are plotted. Qualitative dynamics does not appear to depend on initial conditions.

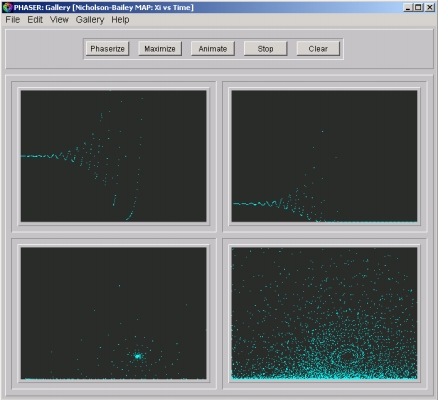
Figure 1. A Gallery of solutions of the Nicholson-Bailey Model.
Click on the image to load it into your local Phaser.

• Figure 2: Fixed point: For relevant parameter values, the system has a fixed point with positive coordinates. This fixed point is unstable (source) and thus cannot be located by trial. However, using the Newton-Raphson method, it is a simple matter to find it. In Figure 2, the first coordinate (host) of the fixed point is plotted as the parameter a is varied.

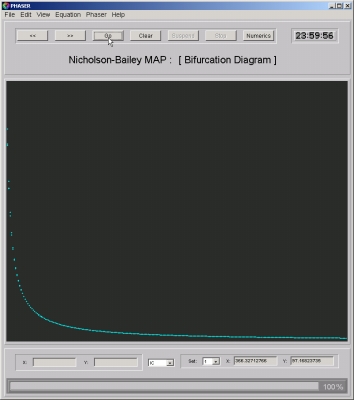
Figure 2. Host equilibrium as the as parameter a is varied.
Click on the image to load it into your local Phaser.

Mathematical results: The planar difference equations have two fixed points: one is always at the origin, and the other at

H^* = (k ln k)/[(k-1)ac],     P^* = (ln k)/a

which depends on the parameters. The latter fixed point is the biologically interesting one (positive coordinates) when k > 1. Linearization at this fixed point yields that the fixed point is unstable for all parameter values k > 1, c > 0, and a > 0.

Experimental data:

Debach and Smith [1941] in their laboratory experiment started with 36 housefly, Musca domestica, and 18 of its pupal parasite Nasonia vitripennis and followed the populations for seven generations. They arranged the fecundity rate of the host to be 2 (k = 2, c = 1), and determined the searching efficiency constant to be a = 0.045.

Varley [1949] used this model to explain fluctuations in the numbers of various species of moths in pine forests.

Burnett [1958] experiments with the greenhouse whitefly, Trialeurodes vaporariurum, with its chalcid parasitoid, Encarsia formosa, provides the closest correspondence (for nearly two dozen generation) with the Nicholson-Bailey model. k = 2, c = 1, a = 0.068, initial host 24, initial parasite 12.

Remarks:

• This model is historically one of the earlier uses of difference equations (MAPs) in modeling populations with non-overlapping generations. It succeeded in providing a quantitative possibility of oscillations in host-parasitoid interactions.
• There is good experimental data to test the model. There is reasonable agreement between the predictions and the data for a dozen or so generations. However, after a few generations, the fluctuations in the sizes of both the host and the parasitoid can get unrealistically large. Moreover, during some generations, parasitoid levels become so low that the model predicts the eventual extinction of the parasitoid.

Suggested Explorations:

1. Alone: Investigate numerically the fate of the host and the parasite in the absence of the other. For this purpose, set the initial density of the absent population to zero. Justify the results of your simulations from the model.
2. Another fixed point: Verify that the origin is a fixed point. Investigate the stability type of this fixed point Discuss the ecological significance of your finding.
3. Load the Phaser Gallery in Figures 1. By changing various parameter values investigate the dependence of dynamics on parameters.
4. Load the Phaser Module in Figures 2. Plot the second coordinate (parasitoid) of the fixed point with respect the parameter a. Plot the coordinates of the fixed point as function of the host growth rate k.
5. Investigate the dynamics for 0 < k ≤ 1, say k = 0.6. What does a typical orbit look like?

Related modules:

Beddington-Free-Lawton MAP: Stabilizing Nicholson-Bailey with host density dependence.

References:

BURNETT, T. [1958]. "A model of host-parasite interaction," Proc. 10th Int. Cong. Ent., 2, 679-686.

DE BACH, P. and SMITH, H.S. [1941]. "Are Population Oscillations Inherent in the Host-Parasite Relation?" Ecology, 22, 363-369. JSTOR URL

EDELSTEIN-KESHET, L. [1988]. Mathematical Models in Biology. Random House, New York.

HASSELL, M.P. [1978]. The Dynamics of Arthropod Predator-Prey Systems. Princeton University Press

HASTINGS, A. [1997]. Population Biology: Concepts and Models. Springer-Verlag New York, Inc.

HSU, S-B., LI, M-C., and MALKIN, M. [2003]. "Heteroclinic Foliation, Global Oscillations for the Nicholson-Bailey Model and Delay of Stability Loss," Discrete and Continuous Dynamical Systems, 9, 1465-1492.

KINGSLAND, S.E. [1995]. Modeling Nature: Episodes in the history of population ecology. University of Chicago Press.

MAYNARD-SMITH, J. [1974]. Mathematical Ideas in Biology. Cambridge University Press.

NICHOLSON, A.J. and BAILEY, V.A. [1935]. "The balance of animal populations," Proceedings of the Zoological Society of London, 1, 551-598.

VARLEY, G.C. [1949]. J. An. Ecol., 18, 117.

Feedback:

Please write to us with your comments about this module.